zimslog
[ML/DL] SVM, Support Vector Machine (서포트 벡터 머신) 본문
[ML/DL] SVM, Support Vector Machine (서포트 벡터 머신)
zimslog 2024. 5. 24. 16:17
이번 포스팅에서는 머신러닝 분류 알고리즘 중 하나인 서포트 벡터 머신(SVM)에 대해 알아보려고 한다.
SVM은 Decision Tree나 인공신경망과 함께 자주 사용되는 분류 기법이며, 특히 이진 데이터(binary data) 분류 문제에서 좋은 성능을 보이는 것으로 알려져 있다.
1. 서포트 벡터 머신 (SVM)
SVM은 데이터를 분류하는 결정 경계(Decision Boundary)을 정의해서 초평면(hyperplane)을 선택하는 알고리즘이다.SVM에 사용되는 몇 가지 개념을 알아보자.
1.1 결정 경계 (Decision Boundary) / 초평면 (Hyperplane)
왼쪽 그림처럼 분류할 집단을 구분하는 속성이 2차원인 경우에는 선(line)으로 두 집단을 구분할 수 있다. 이렇게 집단을 구분하는 경계를 결정 경계 (Decision Boundary)라고 한다.
오른쪽 그림처럼 3차원 형태의 자료에서는 선이 아닌 평면(Plane)으로 집단을 구분할 수 있다.
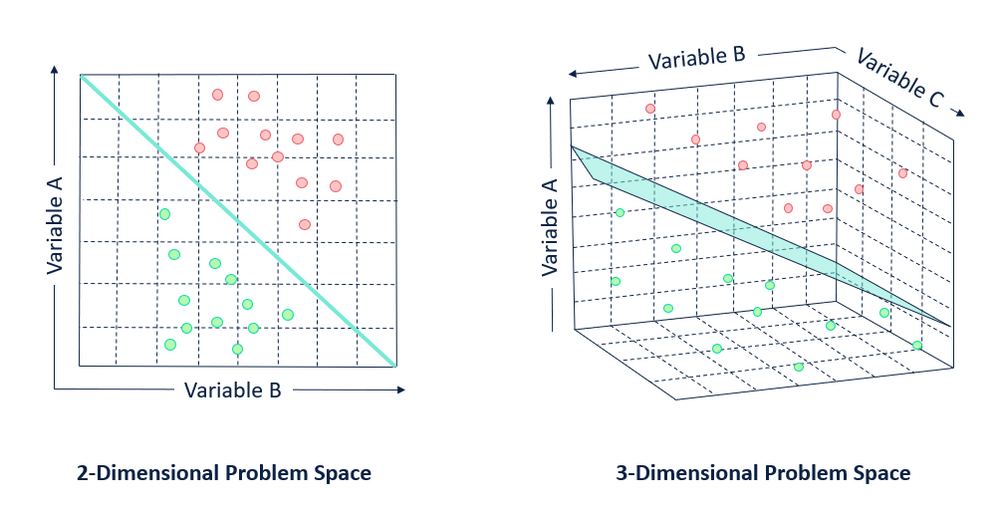
N차원 공간에서의 평면을 초평면(Hyperplane)이라고 하는데, SVM의 목표는 N차원의 공간을 (N-1)차원으로 나눌 수 있는 초평면(Hyperplane)을 찾는 것이다.
1.2 Margin
왼쪽 그림에서 두 집단을 구분하는 선을 찾고자 할 때, 구분선은 여러 개 만들어질 수 있다. 여러 개의 구분선 중 어떤 선을 최적의 결정 경계라고 할 수 있을까? 마진(Margin)이라는 개념을 사용해서 최적의 결정 경계를 찾을 수 있다.
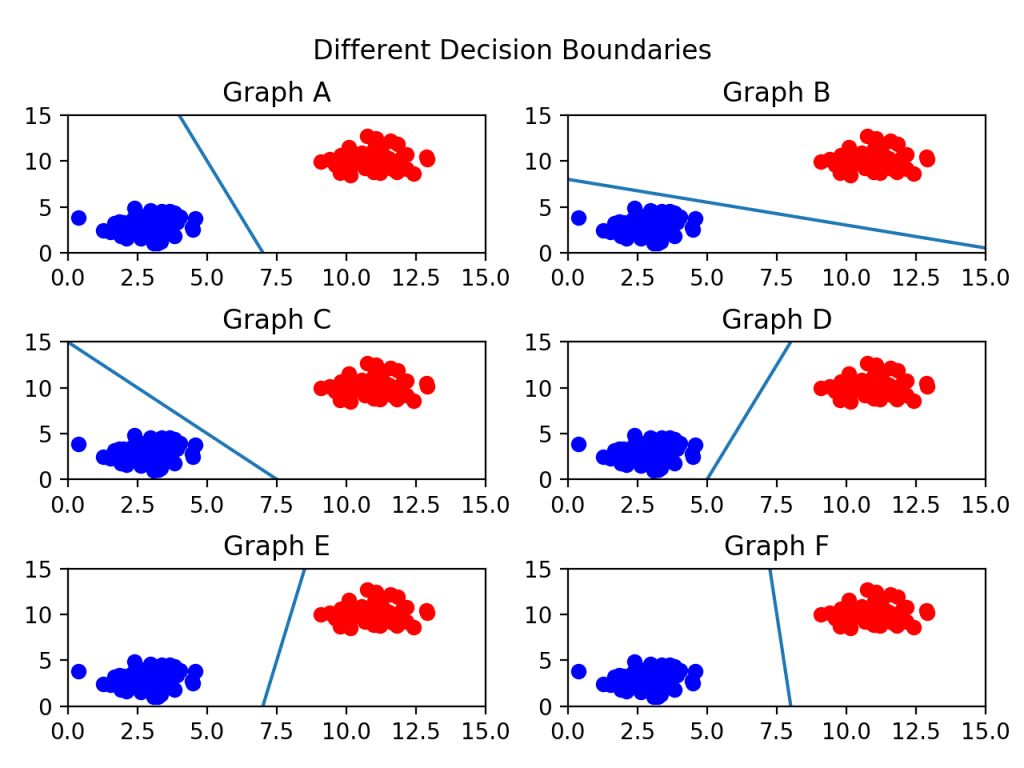
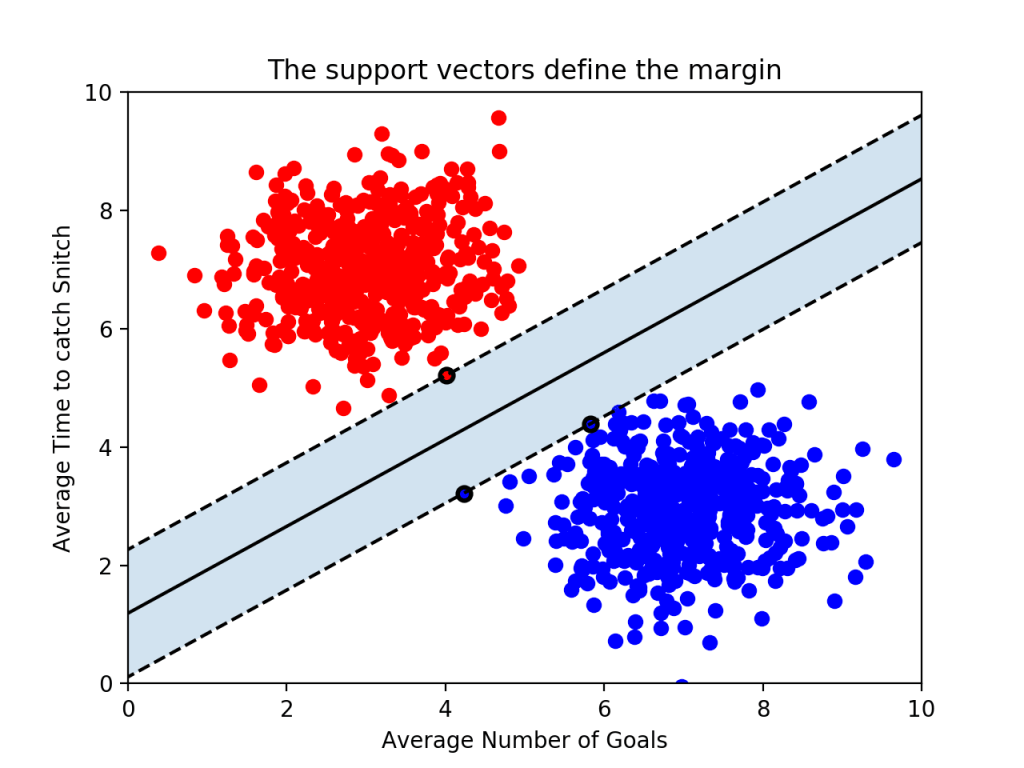
SVM에서 마진(Margin)은 결정 경계와 서포트 벡터* 사이의 거리를 뜻하는데, 오른쪽 그림에서 보면 점선(서포트 벡터)과 실선(결정 경계)까지의 거리가 마진이다.
최적의 결정 경계를 구하기 위해서는 마진이 최대가 되는 경계를 찾아야 하는데, 그 이유는 우리가 원하는 모형은 train set에만 적합한 모형이 아닌 일반화된 모형이기 때문이다.
* 서포트 벡터 : 초평면에 가장 가까이 위치한 데이터 포인트들
마진에는 하드 마진(Hard Margin)과 소프트 마진(Soft Margin) 두 종류가 있다.
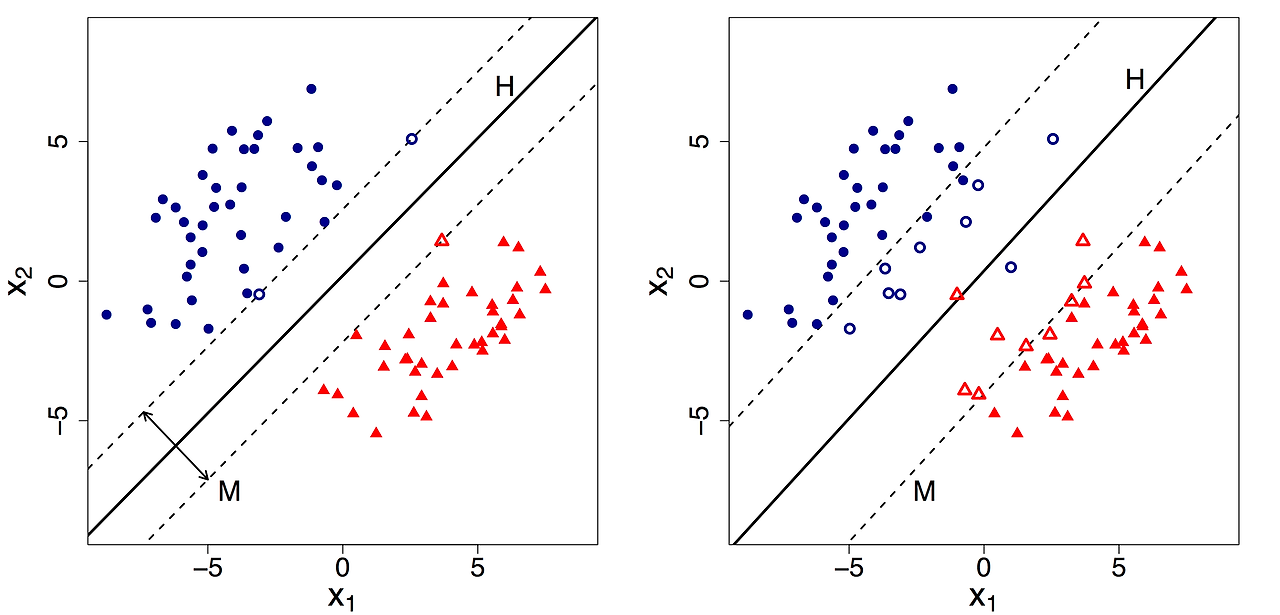
- Hard Margin
데이터가 선형적으로 완벽하게 구분될 수 있는 경우에 사용된다.
실제 데이터에는 노이즈나 겹치는 데이터 포인트가 많기 때문에, Hard Margin은 현실적인 데이터셋에 적용하기 어려울 수 있다. - Soft Margin
Hard Margin의 제약을 완화해서 노이즈가 있는 데이터나 완벽하게 선형 분리가 되지 않는 데이터를 처리할 수 있다. Soft Margin은 일부 데이터가 초평면 가까이 또는 반대 쪽에 위치하는 것을 허용하는데, 여기서 제약 조건을 위반하는 정도를 측정하는 슬랙 변수를 사용한다. 또, 마진과 제약 위반 사이의 균형을 맞추기 위해 매개 변수 $C$를 사용하는데, $C$값에 따라 모델 성능이 크게 달라질 수 있고, 최적 값을 찾기 위해 교차 검증 등의 기법을 사용해야 한다.
2. SVM 작동 원리
2.1 선형 분리 (Linear SVM)
데이터가 선형적으로 분리 가능한 경우에 사용한다. 선형 분리란, 데이터를 하나의 직선 또는 초평면으로 나눌 수 있는 것을 의미한다.
초평면은 직선 또는 평면이므로 아래 식으로 표현 가능하다.
\[ w \cdot x + b = 0 \]
- \( w \) : 초평면의 법 벡터(normal vector)로, 초평면의 방향
- \( x \) : 데이터 포인트 벡터
- \( b \) : 편향(bias) 항으로, 초평면과 원점과의 거리
SVM은 아래 식을 만족하는 최대 마진을 가지는 초평면을 구하게 된다.
\[ \min \frac{1}{2} \|w\|^2 \]
제약 조건: \( y_i (w \cdot x_i + b) \geq 1 \)
- \( y_i \) : 데이터 포인트
- \( x_i \) : 클래스 레이블
2. 비선형 분리 (Non-linear SVM)
비선형 SVM은 데이터가 선형적으로 분리되지 않는 경우에 사용된다.
이런 경우 SVM은 커널 트릭 (Kernel Trick)을 사용해서 데이터를 고차원 공간으로 변환하여 선형적으로 분리할 수 있는 새로운 초평면을 찾는다. 커널 트릭에 사용되는 커널 함수로는 일반적으로 아래와 같은 함수들을 사용한다.
- 다항식 커널 (Polynomial Kernel)
- RBF (Radial Basis Function) 커널
- 시그모이드 커널 (Sigmoid Kernel)
3. Soft Margin SVM
Soft Margin SVM은 노이즈가 있는 데이터나 완벽하게 선형 분리가 되지 않는 데이터를 처리하기 위해 슬랙 변수(\(\xi\))를 사용한다. 이를 통해 일부 데이터 포인트가 초평면에 가까이 있거나 잘못된 쪽에 위치하는 것을 허용할 수 있다.
Soft Margin SVM은 아래 식을 만족하는 최대 마진을 가지는 초평면을 구하게 된다.
\[ \min \frac{1}{2} \|w\|^2 + C \sum_{i=1}^{n} \xi_i \]
제약 조건: \( y_i (w \cdot x_i + b) \geq 1 - \xi_i \)
- \( \xi_i \geq 0 \) : 슬랙 변수
- \( C \) : 제약 위반에 대한 패널티를 조절하는 매개변수
3. SVM 장단점
장점
- 전역 최솟값(global minimun)을 보장한다.
- 선형, 비선형 분류 문제를 모두 다룰 수 있다.
- 소규모 데이터 뿐만 아니라 고차원 데이터에서도 잘 작동한다.
- 소규모 훈련 데이터 셋에서 효과적으로 작동한다.
단점
- 대규모 데이터 셋에서 훈련시간이 길다.
- 클래스가 겹치는 노이즈가 많은 데이터에서는 효과적이지 않다.
- 커널 함수와 매개변수 조정에 민감하다.
- 다중 클래스 문제에 바로 적용하기 어렵고, 여러 이진 분류기를 결합해서 사용해야한다.
'Data Science > Classification' 카테고리의 다른 글
| [ML/DL] GBM, Gradient Boosting Machine (0) | 2024.06.04 |
|---|---|
| [ML/DL] SMOTE 기법 (0) | 2024.02.28 |
| [ML/DL] Imbalanced Data (불균형 데이터 처리) (0) | 2024.02.23 |
| [통계] ROC Analysis (ROC curve, AUC, Optimal cut-off value) (0) | 2024.01.15 |
| [ML/DL] Decision Tree Algorithm (의사결정나무 알고리즘) (0) | 2024.01.10 |



