[ML/DL] 편향(Bias)과 분산(Variance)

 

이번 포스팅에서는 통계학에서 중요한 개념인 편향(bias)과 분산(variance)에 대해 알아보고자 한다.

 

 

1. 편향과 분산

편향이란, 추정 결과가 한쪽으로 치우쳐있는 경향을 말한다.

머신러닝에서는 편향을 통해 예측값들이 정답에서 얼마나 멀리 떨어져 있는지를 나타낼 수 있다.

 

분산이란, 데이터들이 흩어져있는 정도를 의미한다.

머신러닝에서는 분산을 통해 어떤 포인트에 대한 모델 예측 결과의 가변성을 나타낸다.

https://lh3.googleusercontent.com/rq_iMVSuIK1K4ykF9RQnF05hH6xxWm3lmNPWuQ3hfK9r4-3GBIuCxCW3L7QH53M3EIwbVWOcaRiRLDc0AIJ-0uq8-qzavpSWPceQ1lchq-ZPF16l3KLst24-x6MbGYFqQbEJmEI3gEc

 

위쪽 첫 번째 과녁은 모든 결과가 원점에 가깝게 모여져 있다. 이런 경우는 낮은 편향, 낮은 분산을 가진다.

위쪽 두 번째 그림은 모든 결과가 원점 중심으로 퍼져있다. 이런 경우는 낮은 편향을 가지지만 상대적으로 높은 분산을 가진다.

 

아래쪽 첫 번째 그림은 모든 결과가 원점에서 떨어진 거리에 가깝게 모여있다. 이런 경우는 높은 편향, 낮은 분산을 가진다.

마지막 과녁은 원점에서도 먼 거리에 흩어져 있으니, 높은 편향, 높은 분산을 가진다고 할 수 있다.

 

 

 

2. 수식

 

* 편향 (Bias)

$$(E[\hat{f}(x)] - f(x))^2$$

$E[\hat{f}(x)]$ : 예측값들의 평균

$f(x)$ : 정답값

즉, 예측값들의 평균과 정답 값의 차이를 제곱해준 값을 편향이라고 정의한다.

 

 

* 분산 (Variance)

$$E[(\hat{f}(x) - E[\hat{f}(x)])^2]$$

$\hat{f}(x)$ : 예측값

$E[\hat{f}(x)]$ : 예측값들의 평균

즉, 예측값과 예측값들의 평균의 차이를 제곱해서 평균한 값을 분산이라고 정의한다.

 

* 오차 (Error)

$$Error(x) = (E[\hat{f}(x)] - f(x))^2 + E[(\hat{f}(x) - E[\hat{f}(x)])^2] + \sigma^2_e$$

편향과 분산을 더한 값에 $\sigma^2_e$를 더한 값으로 전체적인 오차(Error)를 나타낸다.

$\sigma^2_e$는 존재할 수 밖에 없는 근본적인 오차를 의미한다.

 

 

 

3. 편향과 분산의 Trade-off

편향과 분산은 한쪽이 증가하면 다른 한쪽이 감소하고, 한쪽이 감소하면 다른 한쪽이 증가하는 특징이 있다.

 

또, 머신러닝 모델이 복잡해질수록 편향은 감소하고, 분산은 증가하는 경향을 보이게 된다.

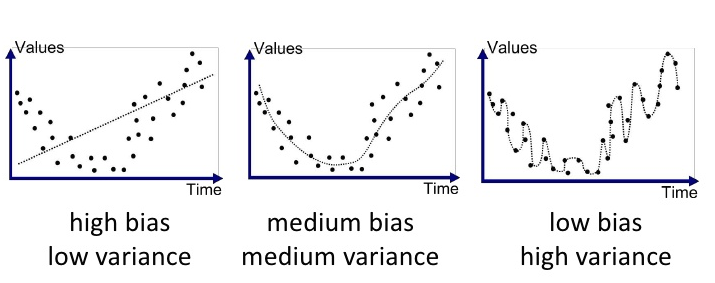
아래 그림을 통해 살펴보자면, 가장 왼쪽 단순한 모델에서는 예측 값과 정답 값의 차이가 크기 때문에 편향이 크고,

예측 값들이 직선위에 나란히 있으니 낮은 분산을 가지게 된다.

 

반면에 가장 오른쪽 복잡한 모델에서는 예측 값과 정답 값에 큰 차이가 없으니 편향이 작고,

예측 값들끼리는 흩어져있으니 높은 분산을 가지게 된다.

이런 모델의 경우 과적합(Overfitting) 문제가 일어날 수 있다.

https://www.opentutorials.org/module/3653/22071

 

 

아래 그래프로 한번 더 확인해보자.

모델이 학습을 반복할수록 모델은 점점 Train dataset을 그대로 외우는 방향으로 학습하게 될 거고,

모델의 복잡도(Complexity)와 과적합(Overfitting) 문제가 일어날 가능성은 점점 증가하게 될 것이다.

 

그래서 Training Error는 계속해서 줄어들겠지만, 어느 지점에서 Validation Error는 거꾸로 상승하게 된다.

우리가 모델을 학습시킬 때는 Validation Error가 최소인 지점에서 훈련을 멈추는 스킬이 필요하다.

https://www.opentutorials.org/module/3653/22071

 

여기까지 편향(bias)과 분산(variance)의 개념과 수식에 대해 알아보았고, 모델 학습 과정에서 이들이 어떻게 변화하는지도 알아보았다. 

 

 

 * Reference

 - https://www.opentutorials.org/module/3653/22071