zimslog
[ML/DL] GLM, Generalized Linear Model (일반화 선형모형) 본문
1. 일반화 선형모형 (GLM)이란?
데이터가 정규 분포가 아닌 임의의 다른 분포를 따르는 경우에 적용할 수 있는 확장된 선형 모형이다.
대표적으로는 로지스틱 회귀, 포아송 회귀 등이 있다.
먼저 정규분포를 가정하는 ordinary linear model에서는 관찰된 예측 변수의 선형 조합으로 반응 변수의 기댓값을 예측한다. 즉, 예측 변수의 일정한 변화는 반응 변수의 일정한 변화를 야기하고 이런 방법은 반응 변수가 정규 분포의 특징을 가지는 경우에 한하여 유용하다고 할 수 있다.
ex)
특정 근사치로부터 어느 방향으로든 다양한 값을 가지는 경우
예측 변수의 변화에 비해 반응 변수의 변화가 상대적으로 작은 경우
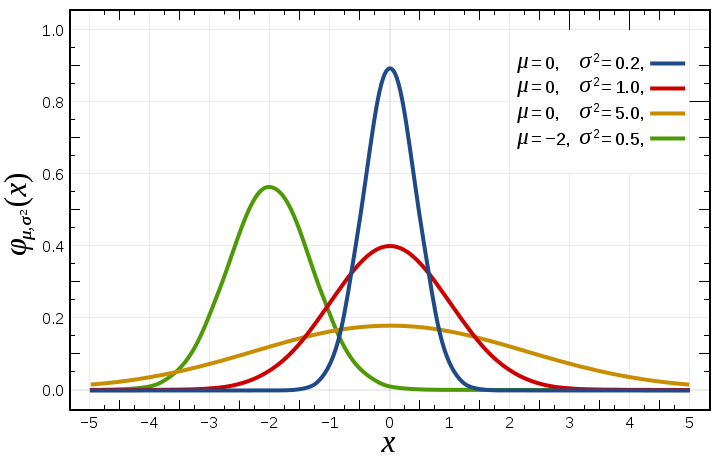
하지만, 데이터가 정규 분포를 따르지 않고 아래와 같은 특징을 가지는 경우에는 확장된 선형 모델인 generalized linear model을 사용하는 것이 바람직하다.
ex)
예측 변수의 일정한 변화가 반응 변수의 매우 큰 변화를 야기는 경우
반응 변수 값의 폭이 매우 큰 경우
반응 변수가 항상 양의 값만을 가지는 경우
...

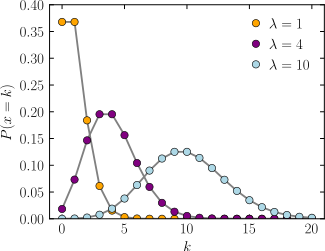
2. 지수족 (Exponential Family)
지수족(Exponential Family)이란 지수함수와 연관되어 있는 특정 확률분포 종류를 가리키는 말로 정규 분포, 감마 분포, 포아송 분포, 지수 분포, 다항 분포 등 일반적으로 널리 사용되는 분포들이 다수 포함되어 있다.
지수족 확률분포의 최대 우도 추정량(MLE)은 유일하게 존재하고 일치성(Consistency)을 만족하며 점근적으로 정규분포(Asymptotic Normal Distribution)를 따른다.
일반화 선형모형(GLM)에서는 반응변수 Y가 지수족의 특정 확률분포를 따른다고 가정한다.
확률 분포를 지수족에서 고려하는 이유는 모형 우도 방정식, 추정량의 점근 분포, 모형 적합 알고리즘에 대한 일반적인 표현식을 얻기 위함이다. 즉, 계산의 편이성을 위해 지수족의 확률 분포 가정을 사용한다.
3. 연결 함수 (Link function)
연결 함수 (Link function) $g$는 선형 예측자 $X\beta$와 반응 변수의 기댓값 $E(y)$를 연결해주는 함수이다.
$$g(E(y)) = X\hat{\beta}$$
연결 함수는 일대일이고 미분가능하며 종류로는 Identity / Log / Reciprocal / Logit / Probit 등이 있다.
일반화 선형모형(GLM)에서는 연결 함수로 변형된 평균이 선형 모형을 따른다는 것을 가정한다.
주의할 점은 연결 함수는 반응변수 y자체를 변형하는 것이 아니라, y의 예측 값인 $\mu_i$를 변형하는 것이다.
log$y_i$ 와 $x_i$ 가 선형 관계라는 말은 log$\mu_i$가 $x_i$와 선형관계 (=일반화 선형 모형)라는 말과는 다르다.
자, 여기까지 일반화 선형 모형에는 아래 두 가지 가정이 있다는 것을 알았다.
1) 반응 변수 y는 지수족의 특정 분포를 따른다.
2) 연결 함수로 변형된 반응 변수 y의 예측값은 선형 모형을 따른다.
단순 선형 모형의 가정과 비교하면 확장된 선형 모형이라는 표현이 잘 와닿는다.
1) 반응 변수 y는 정규분포를 따른다. -> 정규 분포가 아닌 지수족의 분포로 확장
2) 반응 변수 y의 예측값은 설명 변수와 선형 관계를 가진다. -> y 예측값과 설명 변수 관계에 연결 함수 추가
4. 최대우도법 (MLE)
일반화 선형모형은 iteratively re-weighted least squares (IRLS) 방법으로 모델 파라미터를 추정한다.
IRIS는 비선형 회귀 문제를 선형 회귀 문제로 변환하여 해결하는 방식으로, 반복적으로 가중치를 조정하면서 최소제곱법(Least Squares)를 적용한다.
5. 모형 평가
일반화 선형 모형의 파라미터를 추정했다면,
통계적 검정을 통해 모델의 적합도나 모델 파라미터의 유의미함을 확인할 수 있다.
- Wald Test
Wald 검정은 특정 매개변수(또는 매개변수들의 집합)가 통계적으로 유의미한지 여부를 평가하기 위해 사용된다.
주로 회귀 모델에서 각 독립 변수의 계수에 대해 검정을 수행한다.
1. 모델 적합: 데이터를 사용하여 모델을 적합시켜 매개변수 \(\hat{\beta}\)의 추정치를 얻습니다.
2. 표준 오차 계산: 각 매개변수 추정치의 표준 오차 \(SE(\hat{\beta})\)를 계산합니다.
3. Wald 통계량 계산: Wald 통계량은 매개변수 추정치를 그 표준 오차로 나누어 계산됩니다.
\[
W = \frac{\hat{\beta}}{SE(\hat{\beta})}
\]
4. 검정 통계량: Wald 통계량은 표준 정규 분포(또는 t-분포)를 따릅니다. 이 통계량을 이용하여 귀무 가설을 검정합니다.
5. p-값 계산: Wald 통계량의 p-값을 계산하여, 이를 기반으로 귀무 가설을 기각할지 결정합니다.
- 귀무 가설: \(\beta = 0\) (독립 변수가 반응 변수에 영향을 미치지 않는다)
- 대립 가설: \(\beta \neq 0\) (독립 변수가 반응 변수에 영향을 미친다)
- 우도비 검정 (Likelihood Ratio Test, LRT)
우도비 검정은 두 개의 중첩된 모델을 비교하여 더 복잡한 모델이 단순한 모델에 비해 데이터에 더 적합한지 평가하는 데 사용된다.
1. 모델 적합: 두 모델(제약된 모델 \(M_0\)과 제약되지 않은 모델 \(M_1\))을 적합시켜 각각의 최대 우도 \(\mathcal{L}_0\)와 \(\mathcal{L}_1\)를 계산합니다.
2. 우도비 계산: 두 모델의 우도를 비교하는 통계량을 계산합니다.
\[
\lambda = -2 \ln\left(\frac{\mathcal{L}_0}{\mathcal{L}_1}\right) = 2 (\ln\mathcal{L}_1 - \ln\mathcal{L}_0)
\]
3. 검정 통계량: 이 통계량은 자유도 차이만큼의 카이제곱 분포(\(\chi^2\))를 따릅니다.
4. p-값 계산: 카이제곱 분포를 사용하여 검정 통계량의 p-값을 계산하고, 이를 기반으로 귀무 가설을 기각할지 결정합니다.
- 귀무 가설: 단순한 모델이 충분히 데이터를 설명한다.
- 대립 가설: 복잡한 모델이 더 데이터를 잘 설명한다.
'Data Analysis > Regression' 카테고리의 다른 글
| [통계] 회귀 모형 손실 함수 (MAE vs. RMSE vs. MSE) (0) | 2024.03.28 |
|---|---|
| [ML/DL] Regression Model Interpretation (회귀 모델 결과 해석) (0) | 2024.02.14 |
| [ML/DL] Moderated Regression vs. ANCOVA : Interaction (0) | 2024.02.08 |
| [ML/DL] Logistic Regression Analysis (로지스틱 회귀분석) (1) (0) | 2023.11.29 |

