Recent Posts
zimslog
[ML/DL] Decision Tree (의사결정나무) 본문
1. 의사결정나무(Decision Tree)란?
입력 값들의 조합으로 출력 값을 분류, 예측하는 모형으로 트리 구조(Tree)의 그래프로 표현된다.
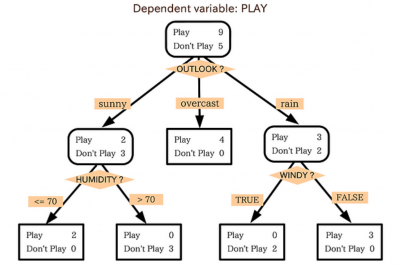
의사결정나무는 분류(classification)와 회귀(regression)가 모두 가능하다.
출력 값이 범주형인 경우나 연속형인 경우 모두 예측 가능하다는 뜻으로,
분류의 경우 해당 terminal node의 종속변수(y)의 최빈값을 예측값으로 반환하고
회귀의 경우 해당 terminal node의 종속변수(y)의 평균을 예측값으로 반환한다.
2. 불순도, 불확실성
나무의 가지를 나누는 기준은 불순도를 통해 정해진다.
분류나무는 구분 뒤 각 영역의 순도(homogeneity)가 증가, 불순도(impurity) 혹은 불확실성(uncertainty)이 최대한 감소하도록 하는 방향으로 학습하고 이 과정을 정보획득(IG, Information gain)이라고 한다.
불순도 지표로는 엔트로피(Entropy)와 지니 계수(Gini index)가 많이 사용된다.
- 엔트로피
$$H(X) = -\sum^{n}_{i=1}p_ilog_2p_i$$
엔트로피는 정보 이론에서 어떤 정보의 불확실성의 정도를 나타낸다.
0~1 사이의 값을 가지며 0에 가까울 수록 정보가 더욱 명확하고 예측 가능함을 뜻한다.
모든 레코드가 동일한 범주에 속할 경우(=불확실성이 최소가 되고, 순도는 최대가 됨) 엔트로피 = 0
반대로 모든 범주의 개체 수가 동일하게 섞여 있을 경우(=불확실성이 최대가 되고, 순도는 최소가 됨) 엔트로피 = 1
- 지니계수
$$Gini = 1-\sum^{C}_{i=1}(p_i)^2$$
엔트로피와 마찬가지로 불순도의 정도를 나타내지만 데이터 분포에 대한 정보를 포함하고 있어 엔트로피보다 더 강력한 특성을 가진다. 0~1 사이의 값을 가지며 지니지수가 작을수록 분기 후 불순도의 감소가 더 크다.
3. 의사결정나무 학습 과정
재귀적 분기(recursive partitioning)와 가지치기(pruning) 두 과정으로 진행된다.
- 재귀적 분기(recursive partitioning)
모든 경우의 수 가운데 정보 획득(IG)이 가장 큰 변수와 그 지점을 택해 첫번째 분기 진행. 이후 또 같은 작업을 반복해 두번째, 세번째… 이렇게 분기를 계속 해 나가는 과정이 의사결정나무의 학습이다. - 가지치기(pruning)
과적합(overfitting)방지를 위해 너무 자세하게 구분된 영역을 통합하는 과정.
모든 terminal node의 순도가 100%인 상태를 Full tree라고 한다.
Full tree를 생성한 뒤 적절한 수준에서 terminal node를 결합하는 과정이 가지치기(pruning)이다.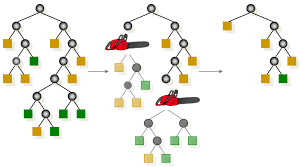
가지가 많아질 수록 새로운 데이터에 대한 오분류율이 감소하나 일정 수준 이상이 되면 오분류율이 오히려 증가한다. 오분류율이 증가하는 시점에서 적절히 가지치기를 수행하여 과적합을 방지해야한다.
4. 의사결정나무 알고리즘
의사결정나무는 아래와 같이 다양한 알고리즘이 존재한다. 각각의 알고리즘에 대한 자세한 설명은 링크된 포스팅으로 따로 다루었다.
- ID3 (Iterative Dichotomiser 3)
- C4.5
- C5.0
- CART (Classification And Regression Tree)
- CHAID (Chi-squared Automatic Interaction Detection)
2024.01.10 - [Data Analysis/Statistics] - [통계] Decision Tree Algorithm (의사결정나무 알고리즘)
5. 장단점
- 장점
- 결과 해석이 쉬우며 의사결정에 직접적으로 활용 가능
- 계산복잡성 대비 높은 예측 성능
- 분류(classification)와 회귀(regression) 모두 가능
- 단점
- 최적해를 보장하지 못함 (Greedy 알고리즘)
- 비연속성 분류
- 결정경계(decision boundary)가 데이터 축에 수직인 데이터에만 최적화
- 데이터의 약간의 변화에 따라 트리 구조가 크게 달라질 수 있음
'Data Science > Classification' 카테고리의 다른 글
| [ML/DL] SMOTE 기법 (0) | 2024.02.28 |
|---|---|
| [ML/DL] Imbalanced Data (불균형 데이터 처리) (0) | 2024.02.23 |
| [통계] ROC Analysis (ROC curve, AUC, Optimal cut-off value) (0) | 2024.01.15 |
| [ML/DL] Decision Tree Algorithm (의사결정나무 알고리즘) (0) | 2024.01.10 |
| [통계] Diagnostic Test (진단 테스트) : Sensitivity, Specificity, Accuracy (민감도, 특이도, 정확도) (0) | 2023.12.07 |


