[통계] Variation Component (변이 구성 요소) (2)

경시적 자료는 한 개체를 반복적으로 관찰하거나 시간의 추이에 따라 표집된 자료이다. 한 개체 내 측정치들 간에 연관성이 존재하므로 공분산이 0이 아니게 되며 변이를 구성하는 요소를 통해 공분산 구조를 추정한다.

 

• 평균 함수를 통한 경시적 자료 표현

$$y_{ij} = \mu(t_{ij}) + \epsilon_{ij}$$

 

 

• 변이를 구성하는 요소

1) 개체 간 변이 (between-individual heterogeneity)

2) 개체 내 변이 (within-individual variation)

3) 측정 오차 (measurement error)

 

 

• 개체 내 변이

1) 자기공분산함수 (Auto-covariance function) : 완전 균형 자료인 경우 (동일한 시점에서 동일한 반복 횟수로 측정된 자료)

2) 변이도 (Variogram) : 일반적인 경시적 자료에서 사용

 

 

1. 자기공분산함수 (Auto-covariance function)

• 자기공분산함수 (Auto-covariance function)

$$\gamma(t, t+u) = cov(Y(t), Y(t+u)) = E[(Y(t)-\mu(t))(Y(t+u)-\mu(t+u))]$$

 

$\gamma(t, t+u) = 0$인 경우, 두 시점 간 반응치들은 독립이다.

 

$\gamma(t, t+u) = 0$ 인 경우, 시점에 상관없이 시간 차(u)에 의해 결정된다. (이차정상성 또는 약한정상성)

 

$\gamma(t, t+u) = 0$ 인 경우, 모든 시점에서의 분산이 같다.

 

• 자기상관함수 (ACF, Auto-correlation function)

$$\rho(u) = \frac{C(u)}{C(0)}$$

 

• 상관도표

$(u, \rho(u))$ 로 그려지는 상관도표

 

 

 

 

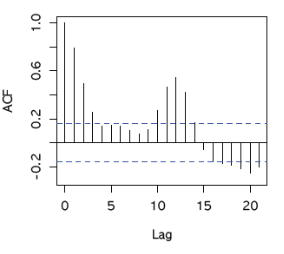
2. 변이도 (Variogram)

: 정상적인 자료에서 효과적으로 사용된다. 자료가 2차 정상과정을 따른다고 가정하고 변이도를 살펴보자.

 

가정) 이차정상성 자료

1. 모든 $t$에 대해 $E[e_t]=0$이다.

2. $cov(e_t, e_{t-d})$는 $d$에만 영향을 받는다.

3. 모든 $t$에 대해 $var(e_t)=\sigma^2$이다.

 

• 변이도 (variogram)

$$\tilde{\gamma}(d) = E[(e_t - e_{t-d})^2] = E[e_t^2] + E[e_{t-d}^2]-2E[e_te_{t-d}] = 2\sigma^2(1-\rho(d))$$

 

• 준변이도 (semi-variogram)

$$\gamma(d) = \tilde{\gamma}(d) /2$$

 

• 상관함수 $\rho$ 정의

• 지수상관모형(exponential correlation) : $\rho(u) = exp(-\phi u)$ 
• 가우스 상관모형(gaussian correlation) : $\rho(u) = exp(-\phi u^2)$