[ML/DL] DNN, Deep Neural Network (심층신경망) (3) - 과적합 (overfitting)

 

2024.04.02 - [Data Science/Deep Learning] - [ML/DL] DNN, Deep Neural Network (심층신경망) (2) - 차원의 저주 (Curse of dimensionality)

[ML/DL] DNN, Deep Neural Network (심층신경망) (2) - 차원의 저주 (Curse of dimensionality)

 

이번 포스팅에서는 DNN 등장 초기의 세 번째 문제점 과적합(Overfitting)에 대해 알아보겠다.

 

1. 과적합 (Overfitting)

과적합은 말그대로 모델이 학습 데이터(Train-set)를 과하게 학습했다는 것을 뜻한다.
이런 경우는 모델이 적절하게 일반화되지 않아서 미확인 데이터에 대해서는 낮은 성능을 보이게 된다.

 

 
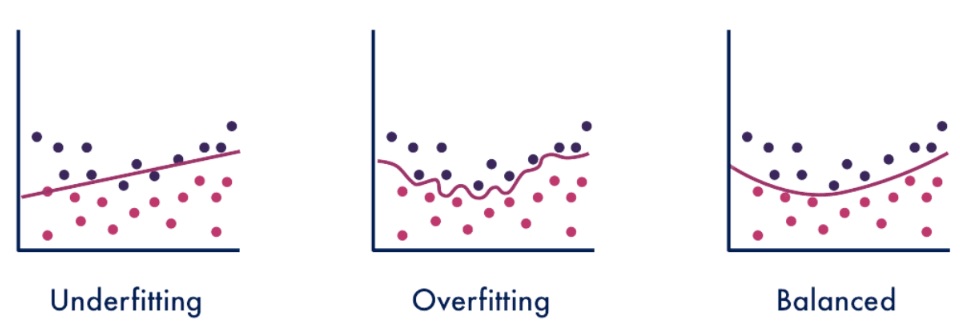
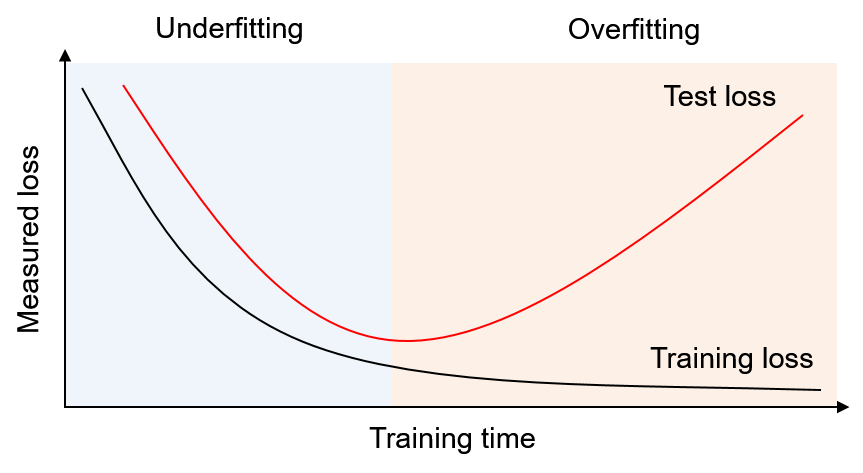
위 그림에서 두 곡선은 학습 시간에 따른 train-set의 예측 오차와 test-set의 예측오차를 나타낸다.
 
하늘색 구간에서는 학습이 진행됨에 따라 두 개의 예측오차가 함께 감소하는데, 이 구간에서는 모델이 부족하게 학습되었다 즉, 과소적합(under fitting) 되었다고 한다.
 
분홍색 구간으로 넘어가면 train-set 예측 오차는 계속 감소하는 반면, test-set 예측오차가 증가하는 것을 확인할 수 있는데, 모델이 학습데이터에 대해 과도하게 학습하게 되면서 미확인 데이터에서는 낮은 성능을 보이게 되는 것이다.
이런 경우를 모델이 과적합(overfitting) 되었다고 한다.
 
과적합은 학습할 데이터가 부족하거나 모델이 복잡할 때 발생한다. 그렇다면 DNN 같이 복잡한 모델에서 과적합 문제를 어떻게 해결해야 할까?

 

학습 데이터를 늘리는 방법도 있겠지만, 실제 연구에서는 활용할 수 있는 데이터 양이 한정적인 경우가 많기 때문에 여러 방법들을 고려해야할 필요가 있다.
 

2. 과적합 해결방법

• 데이터 증강 (data augmentation)
  영상 데이터 같은 경우는 비율을 변경하거나, 일부분을 가리거나, 여러 방향으로 회전시키는 등의 방식으로 데이터 수를 늘릴 수 있다.
  이외에도, deformable 영상 변환을 시도하거나 인위적인 noise를 추가해서 품질에 variance를 주는 방법도 있다.
  
  
• L1/L2 정규화 (L1/L2 regularization)
  손실함수(Loss function)에 regularization term을 넣어서 weight가 과도하게 조정되지 않게 만드는 방법이다.
  기존 손실함수에 가중치의 크기가 포함되면서 패널티를 주는 방식으로 가중치가 너무 크지 않게 학습되도록 한다.
  $$L = L_{error} + \frac{\lambda}{2}|W|^2$$
  
  
• Dropout
  학습 과정에서 일정 비율의 임의 node에 대해서는 weight를 조정하지 않는 기법이다.
  이 방법은 머신러닝의 앙상블 방법과도 유사한데, 실제로도 DNN 학습과정에 dropout을 적용하면 앙상블 효과를 낸다는 것이 증명되기도 했다.
  
  
  

여기까지 세 개의 포스팅에 걸쳐 DNN의 초기 문제점들과 해결 방법에 대해 알아보았다.
다음 포스팅부터는 컨볼루션 신경망(Convolutional neural network)을 시작으로 여러 신경망 기법들에 대해 알아보겠다.

 

2024.04.05 - [Deep Learning] - [DL] CNN, Convolutional Neural Network (컨볼루션 신경망)

[DL] CNN, Convolutional Neural Network (컨볼루션 신경망)